Die Korrelieren Definition beschreibt, wie verschiedene Variablen zusammenhängen. Es ist ein wichtiger Begriff in der Statistik. Durch das Verstehen dieser Zusammenhänge können wir Muster in Daten erkennen.
Korrelationen sind sehr wichtig, um Daten zu analysieren und Vorhersagen zu treffen.
Ein einfaches Beispiel ist die Beziehung zwischen Lernzeit und Testnote. Je mehr man lernt, desto besser sind die Noten. Diese Analyse hat ihre Wurzeln in der Geschichte der Statistik.
Schlüsselerkenntnisse
- Korrelieren beschreibt den Zusammenhang zwischen Variablen.
- Korrelation kann Werte zwischen -1 und 1 annehmen.
- Positive Korrelation bedeutet, dass Werte gleichzeitig steigen.
- Ein Korrelationskoeffizient von 0 zeigt keinen Zusammenhang an.
- Die Korrelationsanalyse ist entscheidend für fundierte Entscheidungen.
Korrelation: Ein Überblick
Die Korrelation zeigt, wie stark und in welche Richtung zwei Variablen zusammenhängen. Sie ist wichtig in vielen Bereichen. Zum Beispiel, wenn Jungen größer sind, bekommen sie oft bessere Noten.
Manchmal ist die Korrelation negativ. Zum Beispiel, wenn Menschen kleiner werden, steigen ihre Noten.
Ein Beispiel für Korrelationen sind Einwohnerzahlen in Städten. In dichteren Städten gibt es oft mehr Reisen. Aber das sagt uns nicht, dass Reisen die Stadtgröße verursacht.
Ein weiteres Beispiel ist der Bitcoin-Preis. Seit Anfang des Jahres ist er um 150 Prozent gestiegen. Im Vergleich zum S&P 500 hat Bitcoin in den letzten zehn Jahren besser abgeschnitten. Aber die Korrelation zwischen beiden war meist unter 0,2.
Seit der Pandemie ist die Korrelation zwischen Bitcoin und S&P 500 gestiegen. Das liegt an den Schwierigkeiten mit Anlagen während der Pandemie.
Tools wie tidycomm-Paket helfen, Korrelationen zu visualisieren. Das macht es einfacher, Daten zu analysieren und Ergebnisse zu verstehen. Durch Visualisierungen wird die Komplexität von Korrelationen klarer.
Korrelieren Definition
Um die Beziehungen zwischen verschiedenen Variablen zu verstehen, ist es entscheidend, die Korrelation zu definieren. Diese mathematische Beziehung beschreibt, wie stark und in welcher Richtung zwei Variablen miteinander verbunden sind. Ein essenzielles Konzept in der Statistik, bietet die Korrelation Entscheidungsgrundlagen in vielen wissenschaftlichen und praktischen Anwendungen.
Was ist Korrelation?
In der Definition ist eine Korrelation ein Maß für die Stärke und Richtung des Zusammenhangs zwischen zwei oder mehreren Variablen. Positive Korrelationen zeigen, dass ein Anstieg einer Variable gleichzeitig mit einem Anstieg einer anderen Variable einhergeht. Eine negative Korrelation indiziert ein inverses Verhältnis, wo eine Zunahme einer Variable zu einer Abnahme der anderen führt. Statistische Techniken, wie der Pearson–Korrelationskoeffizient, werden häufig zur Analyse dieser Zusammenhänge verwendet.
Die Bedeutung der Korrelation in der Statistik
Die statistische Bedeutung von Korrelationen ist weitreichend. Statistiker nutzen Korrelationen, um quantitativen Einblicke in komplexe Datensätze zu gewinnen. In vielen Disziplinen, von der Physik bis zu den Sozialwissenschaften, spielen Korrelationen eine zentrale Rolle bei der Analyse von Hypothesen. Besonders in der Festkörperphysik helfen sie bei der Erforschung von Materialeigenschaften auf mikroskopischer Ebene, was ihrer Allgegenwärtigkeit in der Forschung Nachdruck verleiht.
Arten von Korrelationen
Es gibt verschiedene Arten von Korrelationen. Sie helfen uns, die Beziehungen zwischen Variablen zu verstehen. In der Statistik sind sie sehr wichtig. Die häufigsten sind positive und negative Korrelationen.
Positive und negative Korrelation
Eine positive Korrelation zeigt, wenn beide Variablen gleichzeitig steigen. Zum Beispiel steigt der Verbrauch mit dem Wirtschaftswachstum. Eine negative Korrelation bedeutet, dass eine Variable steigt, während die andere fällt. Zum Beispiel steigt das Alter, während die Lebenserwartung sinkt.
Beispiele für Korrelationen in verschiedenen Bereichen
In der Wirtschaft steigt das Angebot mit dem Nachfrage. In der Gesundheitsforschung sinkt die Lebensqualität mit mehr Zigaretten. In den Sozialwissenschaften helfen Korrelationen, Muster zu finden.
Korrelationskoeffizient: Messung und Bedeutung
Der Korrelationskoeffizient misst, wie stark zwei Zahlenwerte miteinander verbunden sind. Er ist sehr wichtig in der Forschung und hilft uns, Zusammenhänge zu verstehen. Der Wert kann von -1 bis +1 liegen. -1 zeigt eine negative, +1 eine positive Korrelation. Ein Wert von 0 bedeutet, es gibt keine Korrelation.
Was ist der Korrelationskoeffizient?
Er zeigt, wie eine Veränderung in einer Zahl mit einer Veränderung in einer anderen verbunden ist. Ein hoher positiver Wert bedeutet, dass beide Zahlen steigen. Ein hoher negativer Wert zeigt, dass eine steigt und die andere fällt.
Es ist wichtig zu wissen, dass Korrelation nicht bedeutet, dass eine Zahl die andere verursacht. Eine Veränderung in einer Zahl führt nicht immer zu einer Veränderung in der anderen.
Berechnung des Pearson-Korrelationskoeffizienten
Der Pearson-Korrelationskoeffizient ist eine beliebte Methode zur Berechnung. Er nutzt die Summe der Zahlen, die Summe der Quadrate und das Produkt der gepaarten Werte. Die Formel ist komplex und erfordert mehrere Schritte.
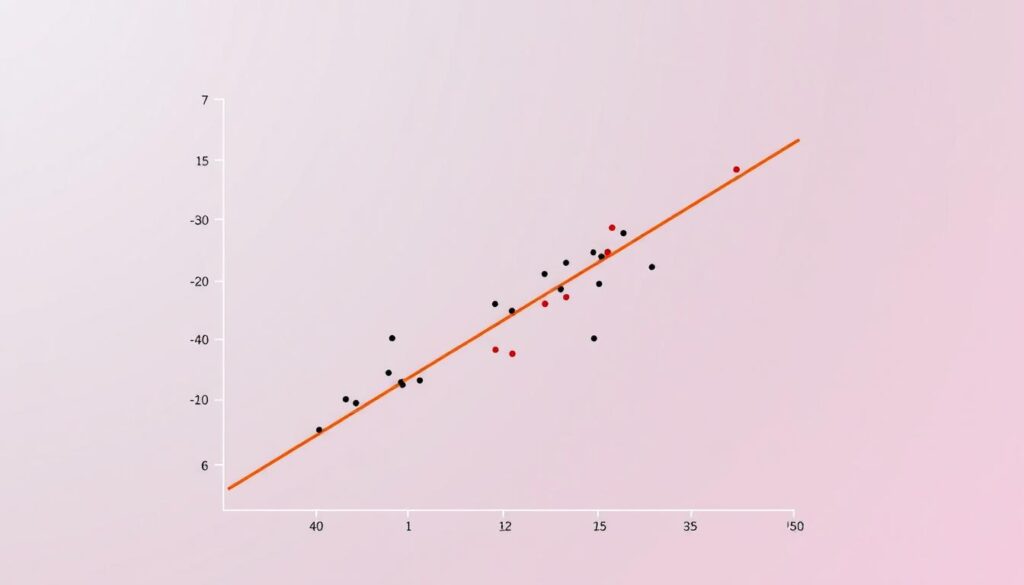
Ein Streudiagramm hilft, die Beziehung zwischen den Zahlen zu sehen. Es zeigt, ob die Pearson-Korrelation passt.
Korrelationsanalyse: Anwendungen und Nutzen
Die Korrelationsanalyse ist ein nützliches Werkzeug in vielen Bereichen. Dazu gehören Wirtschaft, Gesundheitswesen und soziale Wissenschaften. Sie hilft dabei, Muster und Beziehungen zwischen Variablen zu finden. Das ist sehr wichtig für die Entscheidungsfindung.
Praktische Anwendungen der Korrelationsanalyse
In der Wirtschaft kann man damit Zusammenhänge zwischen Verkaufszahlen und Werbung erkennen. In der Medizin hilft sie, Beziehungen zwischen Behandlungen und Patientenergebnissen zu finden. Diese Anwendungen verbessern Strategien und Verfahren in diesen Bereichen. Mehr Infos gibt es hier.
Vorteile der Korrelationsanalyse in der Forschung
Die Korrelationsanalyse ist sehr nützlich in der Forschung. Sie hilft, Hypothesen zu prüfen und Zusammenhänge zu finden. Sie ermöglicht es, komplexe Phänomene besser zu verstehen und neue Forschungsansätze zu entwickeln.
Es ist wichtig, den richtigen Korrelationskoeffizienten zu wählen. So bekommt man präzise Ergebnisse. Verschiedene Arten von Korrelationen können je nach Forschungsfrage ausgewählt werden, um gute Erkenntnisse zu erzielen.
| Anwendung | Bereich | Mehrwert |
|---|---|---|
| Identifikation von Verkaufsmustern | Wirtschaft | Verbesserung der Marketingstrategien |
| Analyse von Behandlungsansätzen | Gesundheitswesen | Optimierung patientenorientierter Therapien |
| Studie von sozialen Trends | Soziale Wissenschaften | Verständnis komplexer gesellschaftlicher Strukturen |
Vorbereitung der Daten für die Korrelationsanalyse
Die Vorbereitung der Daten ist sehr wichtig für eine erfolgreiche Korrelationsanalyse. Es beginnt mit der Datenerhebung aus vertrauenswürdigen Quellen. Danach prüft man die Daten auf Qualität und Integrität.
Man sucht nach fehlenden Werten und Ausreißern. So wird sichergestellt, dass die Daten für eine zuverlässige Analyse geeignet sind.
Datenerhebung und -prüfen
Bei der Datenerhebung für die Korrelationsanalyse muss man vorsichtig sein. Es ist wichtig, alle relevanten Variablen zu berücksichtigen. Die Daten müssen vollständig und genau sein.
Man kann dies durch Ansehen oder statistische Tests überprüfen. So findet man Probleme früh.
Datenbereinigung und Umgang mit Ausreißern
Nach der Datenerhebung kommt die Datenbereinigung. Hier werden fehlende Werte behandelt. Man kann sie durch Imputation oder das Entfernen ersetzen.
Ein wichtiger Schritt ist der Umgang mit Ausreißern. Diese extremen Werte können die Ergebnisse stark beeinflussen. Es ist entscheidend, ob man sie einbezieht oder nicht.
Eine sorgfältige Datenbereinigung macht die Ergebnisse verlässlicher. So vermeidet man Verzerrungen in den Interpretationen.
Die richtige Vorbereitung der Daten ist entscheidend. So wird die Korrelationsanalyse erfolgreich durchgeführt.
Interpretation von Korrelationen
Die Interpretation von Korrelationen ist sehr wichtig. Sie hilft uns, die Analyseergebnisse zu verstehen. Der Korrelationskoeffizient zeigt, wie stark zwei Variablen miteinander verbunden sind. Werte zwischen -1 und 1 geben uns genauere Infos.
Ein Wert von +1 bedeutet eine perfekte positive Korrelation. -1 zeigt eine perfekte negative Korrelation. Ein Wert von 0 bedeutet, dass keine Korrelation erkennbar ist.
Es gibt verschiedene Arten von Korrelationen. Zum Beispiel lineare und nichtlineare Korrelationen. Die Wahl der Korrelation beeinflusst, wie wir die Daten interpretieren.
Die bivariate Korrelationsanalyse betrachtet die Beziehung zwischen zwei Variablen. Die multiple Korrelationsanalyse sieht die Wechselwirkungen zwischen einer abhängigen und mehreren unabhängigen Variablen.
Ein hoher Korrelationskoeffizient zeigt eine starke Beziehung. Ein niedriger Koeffizient bedeutet eine schwache Verbindung. Aber wir müssen vorsichtig sein, denn Korrelation bedeutet nicht immer Kausalität.
Bei der Analyse helfen Software-Tools wie Excel oder Python. Sie machen die Berechnung des Korrelationskoeffizienten einfacher.
Die folgende Tabelle zeigt die wichtigsten Merkmale verschiedener Korrelationsarten:
| Korrelationstyp | Definition | Berechnungsmethode |
|---|---|---|
| Pearson-Korrelation | Bewertet die lineare Beziehung zwischen zwei Variablen. | Formel für den Pearson-Korrelationskoeffizienten. |
| Spearman-Korrelation | Untersucht monotone Beziehungen basierend auf Rangwerten. | Formel, die Rangdifferenzen berücksichtigt. |
| Bivariate Korrelation | Analyse der Beziehung zwischen genau zwei Variablen. | Direkte Berechnung der Korrelation. |
| Multiple Korrelation | Analyse der Beziehung zwischen einer abhängigen und mehreren unabhängigen Variablen. | Komplexe Modelle zur Analyse. |
Fazit
Korrelationen und Korrelationsanalysen sind sehr wichtig für die Datenanalyse. Sie helfen uns, die Beziehungen zwischen Variablen zu verstehen. So können wir genaue Vorhersagen machen und kluge Entscheidungen treffen.
Die Bedeutung der Korrelation ist in vielen Bereichen anerkannt. In der Wissenschaft, Wirtschaft und anderen Feldern ist sie unverzichtbar.
Der Korrelationskoeffizient „r“ zeigt uns, wie stark zwei Variablen miteinander verbunden sind. Er reicht von -1 bis +1. Ein positiver Wert bedeutet, dass die Variablen direkt zusammenhängen.
Dies ist besonders wichtig im Marketing und bei der Planung. Positive Korrelationen helfen uns, bessere Entscheidungen zu treffen.
Korrelationsanalysen sind auch wichtig für das Risiko-Management und die Qualitätssicherung. Sie können sogar zu großen Entdeckungen führen. Korrelationsanalysen sind ein grundlegendes Werkzeug in vielen Bereichen.
Weitere Infos zur Korrelationsanalyse gibt es hier.




